文章目录
- 前言
- 轮转数组😎
- 寻找奇数😎
- 数组中数字出现的次数😎
- 结尾
前言
刷题笔记第一道题跟后面没啥关系
但是后两道关系比较明显
最后一道题看不懂的朋友请多看看倒数第二道题
轮转数组😎
连接
一个规律=-=而非思想,叫
三趟逆置法
想要旋转数组元素的前K个只需要
先逆置N-K项
再逆置K项
再整体逆置
首先说一下旋转和逆置的区别
以数组: 1,2,3,4,5,6,7,8为例
旋转3次可以理解就成为4,5,6,7,8,1,2,3
而逆置前三个元素就是 3,2,1,4,5,6,7,8
逆置前四个元素就是4,3,2,1,5,6,7,8
可以理解为逆置就是将要逆置的元素首位交换位置
而旋转就是将要旋转位数的元素前移(右旋转)或后移(左旋转)其他元素向后移动.
所以逆置要比旋转轻松很多
我们使用的三趟逆置法就是一个规律----如果感觉必要的话可以背一下=-=.
void reverse(int* nums,int left,int right){ while (left < right) { int ret = nums[left]; nums[left] = nums[right]; nums[right] = ret; left++; right--; }}void rotate(int* nums, int numsSize, int k){ k %= numsSize; reverse(nums, 0, numsSize - k - 1); reverse(nums, numsSize - k , numsSize - 1); reverse(nums, 0, numsSize - 1);}说这么多还是代码见真章
其中
void reverse(int* nums,int left,int right);这个函数是逆置的,你只需将要逆置的数组和左右位置下标传给他就好没啥讲的.
void rotate(int* nums, int numsSize, int k);该函数是我们要实现的接口函数我们只需注意k的取值因为当k大于numsSize时多余的次数只是在循环,所以我们可以使用k%=numsSize来避免越界和效率的浪费.
寻找奇数😎
1、现在有一个长度为 n 的正整数序列,其中只有一种数值出现了奇数次,其他数值均出现偶数次,请你找出那个出现奇数次的数值。
输入描述:第一行:一个整数n,表示序列的长度。第二行:n个正整数ai,两个数中间以空格隔开。
输出描述:一个数,即在序列中唯一出现奇数次的数值。
OJ链接【牛客网题号:KS33 寻找奇数】【难度:简单】
答案:
int main(){ int n = 0; scanf("%d", &n); int k = 0; int ans = 0; for (int i = 0; i < n; i++) { scanf("%d", &k); ans ^= k; } printf("%d",ans); return 0;}思路: 按位异或操作符的应用
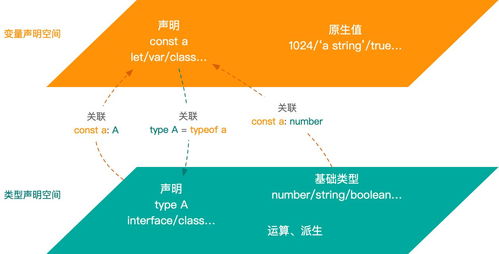
下面先介绍一下原理
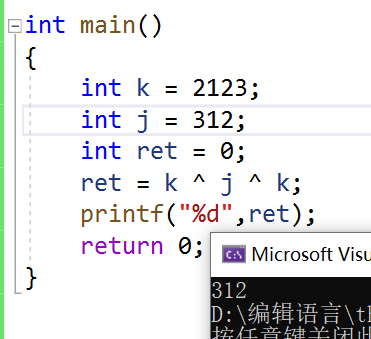
从上图可以看出
① 0^k(随便一个数) = k;
^操作的两个数在二进制中相同就为0相异就为1
② k^k = 0;(甚至可以隔着几个数依旧成立)如上图的k^j^k = j
知道这两个原理就可以做出本题了
我们要从数值里找到一个出现数次为奇数的值.就原理②可以看到出现偶数次的数值通过按位异或就变成0 出现次数为奇数的数值就会和答案里的ans(及0)进行按位异或操作得到奇数数值最后打印即可
我们再来看一下答案就能更清楚的明白了.
int main(){ int n = 0; scanf("%d", &n); int k = 0; int ans = 0;//因为0按位异或任何数都是那个数值 for (int i = 0; i < n; i++) { scanf("%d", &k); ans ^= k;//使用^= 时要注意ans一定要初始化为0才能将k保存下来用来下一次的操作 } printf("%d",ans);//最后只有出现为奇数的值被保留了下来 return 0;}数组中数字出现的次数😎
连接
上一道题我们通过^操作符完成的,这道题也用^不过会稍微更有难度一些.
首先代码奉上.解析在代码下.
int* singleNumbers(int* nums, int numsSize, int* returnSize){ int i = 0; int x = 0; for (i = 0; i < numsSize; i++) { x ^= nums[i]; } int num = 0; for (i = 0; i < 32; i++) { if (((x >> i) & 1) == 1) { num = i; break; } } int m = 0; int n = 0; for (i = 0; i < numsSize; i++) { if (((nums[i] >> num) & 1) == 1) { m ^= nums[i]; } else { n ^= nums[i]; } } int* ret = (int*)malloc(sizeof(int) * 2); *returnSize = 2; ret[0] = m; ret[1] = n; return ret;}这道题也有别名叫寻找单身狗,是在数组中寻找两个单身的数组,因为是两个所以我们不能想之前那样直接使用^我们需要先将所有数值与x进行^操作这是为了得到两个单次出现数组的^值比如{1,1,3,3,2,2,5,6,7,7,6,9}单次出现的数字为5,9
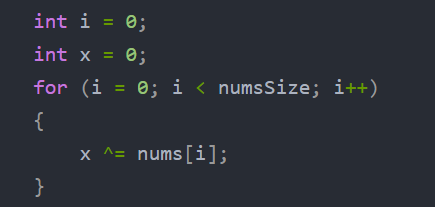
这样我们的x值其实就相当于5^9的值在得到这个之后我们需要进行分组,而分组我们就需要将5和9分开,有什么条件可以让5和9分开呢?
这里我们就要用到
^在二进制位相同为0相异为1
所以我们只需要找到x在那一二进制位为1就好.
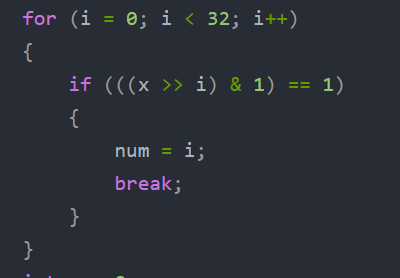
这一步就是为了得到二进制位1的位置
得到后我们就可以通过这个位数的1将两个单身狗分开分别进行^操作得到这两个单身狗了.
结尾
求三连,求点赞,我想要机器人😭