►宇称-时间对称的量子行走的相图及观测拓扑保护边界态实验装置图,图片截自Xiao et al, 2017
http://
nature.com
薛鹏教授团队首先设计了开放系统中loss-no loss量子行走模型,以交替的损耗-不损耗的方式取代难以实现的损耗-增益,并证明其满足宇称-时间对称性。他们利用单光子在线性光学体系中实现了宇称-时间对称的量子行走,分别演示了这种对称性保持、破缺以及临界点的量子特性,首次实现了真正意义上的宇称-时间对称的量子系统的动力学演化过程。接下来,薛鹏教授团队进一步研究开放系统的量子行走的特殊性质和应用。

封闭系统中量子行走的演化是幺正的,并且具有particle-hole、时间反演和手性三种对称性,这为研究Floquet拓扑相提供了一个理想的平台。开放系统中,时间反演对称和手性对称均破缺,是否存在Floquet拓扑相一直是一个悬而未决的问题。薛鹏教授团队研究发现,宇称-时间对称的量子行走也存在三种对称性,即宇称-时间、宇称-手性和particle-hole对称。
在此驱动下,非幺正的量子行走同样存在Floquet拓扑相,而其bulk拓扑性质可由一对拓扑不变量来表征。
在解决这一理论难题后,该团队又要面对实验上如何全面且清楚地表示拓扑性质及新的物态这一挑战。经过反复的论证,该团队通过控制量子行走的参数,发现在具有不同bulk拓扑性质的区域的边界存在源于Floquet拓扑相的边界态,同时可以通过宇称-时间对称的量子行走的动力学演化结果观测到拓扑边界态。由于开放系统的特性,动力学演化过程展现出与幺正量子行走截然不同的结果。
例如,几率分布呈现局域化,而在参数空间边界的位置的有效几率随演化时间增长而增长。薛鹏教授团队在实验中还观测到两类不同的拓扑边界态的存在,其对量子行走的动力学演化的作用随时间交替呈现,而这则是Floquet拓扑相的特征。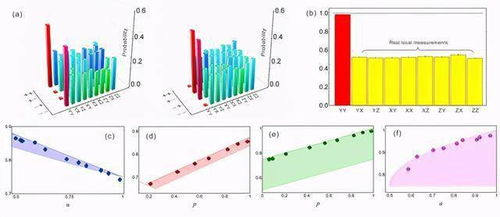
与此同时,通过分别引入宇称-时间对称保持的扰动和宇称-时间对称破缺的无序失调,实验证实了拓扑边界态对这两种情况均表现出很强的鲁棒性。
这是因为无序失调虽然导致宇称-时间对称破缺,但是依然存在一种更为普适的对称性(即pseudo-unitarity),对拓扑边界态起到保护作用。这也是迄今首次实验证实pseudo-unitarity这种对称性的存在。