这里是目录

• 前言
• 一、插入排序
• • 1.排序思路
  • 2.单趟排序
  • • (1).详细图解
  • 3.整体代码
  • 4.时间复杂度
  • • (1).最坏情况下
    • (2).最好情况下
    • (3).基本有序情况下(重点)
  • 5.算法特点
• 二、希尔排序
• • 1.希尔从哪个方面优化的插入排序？
  • 2.排序思路
  • 3.预排序
  • 4.正式排序
  • 5.整体代码
  • 6.时间复杂度
  • • (1).while循环的复杂度
    • (2).每组gap的时间复杂度

前言

学习希尔排序要先学习插入排序，希尔排序是在插入排序上的优化，可以这么说，插入排序你只要会了，希尔排序的学习也就是水到渠成。

一、插入排序

假如给你以下代码，让你对 5 4 3 2 1 排升序，你会怎么排？会怎么写？

5 4 3 2 1

void InsertSort(int* a, int n){	//排序代码}int main(){	int arr[] = { 5,4,3,2,1 };	int sz = sizeof(arr) / sizeof(arr[0]);	InsertSort(arr, sz);	return 0;}

1.排序思路

思路：总体来说是分治思想，把大问题化为小问题来解决。想让5,4,3,2,1有序。
1.第一趟：从下标为1的位置依次往后开始，先让5,4为升序
2.第二趟：来到下标为2的位置，让5,4,3为升序
3.第三趟：来到下标为3的位置，让5,4,3,2为升序
4.第四趟：来到下标为3的位置，让5,4,3,2,1为升序

这样下来，总体就都为升序了
所以总体来说，在最坏情况下。5个数排了(5-1)躺就有序了.
所以最坏情况下n个数排n-1躺才能有序。

2.单趟排序

万物归根，学习任何排序先从单趟排序开始。
可以说关键思想在单躺排序中。

以第三趟排序为例。因为这趟排序有画图意义
思路：
第三趟：来到下标为3的位置，让5,4,3,2为升序

1.起始状态。因为能走到第三趟排序，说明第一趟和第二趟已经排好序了，以红色线分割这时的数据为3 4 5 2 1

2.定义指针end指向有序序列的最后一个数，让tmp保存end+1位置的值。(这样可以防止end+1指向的值被覆盖后找不到)

3.开始打擂台赛。比较tmp的值和end的值的大小，然后end–。把比tmp大的值依次往后挪动。直到 end < 0越界 或者 tmp比end指向的值大时，单趟排序才完成。

(1).详细图解

(1). tmp为 2 小于 5, 执行a[end+ 1] = a[end];把end+1上的值覆盖。end = end - 1。

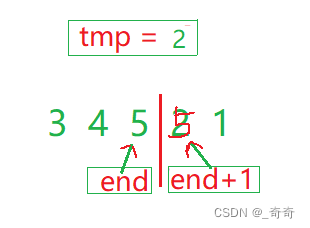
(2). 2小于 4，继续重复以上步骤。
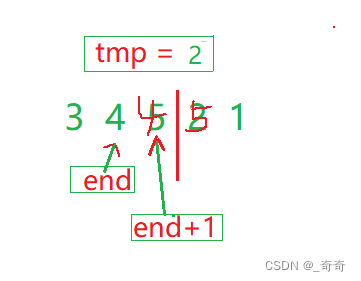(3).2小于 4，继续重复以上步骤。

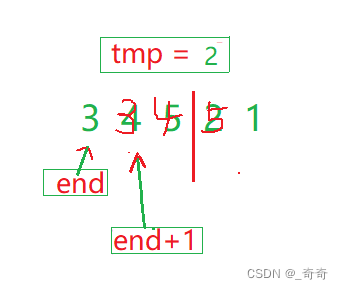
(4).end此时越界。直接跳出循环，将tmp赋值给a[end + 1];
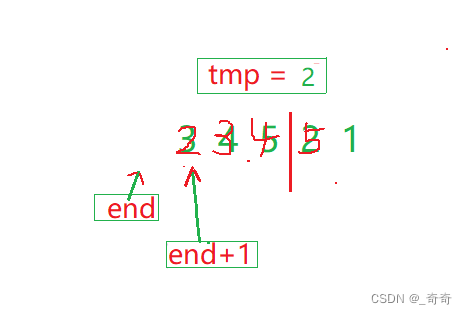这样就完成了单趟排序的解释。

3.整体代码

#include <stdio.h>void InsertSort(int* a, int n){	int i = 0;	//总共n-1躺排序	for (i = 0; i < n - 1; i++)	{		//单趟排序		int end = i;		int tmp = a[end + 1];		while (end >= 0)		{			//打擂台赛			if (tmp < a[end])			{				a[end + 1] = a[end];				end = end - 1;			}			else			{				break;			}		}		a[end + 1] = tmp;	}}int main(){	int arr[] = { 5,4,3,2,1 };	int sz = sizeof(arr) / sizeof(arr[0]);	InsertSort(arr, sz);	return 0;}

4.时间复杂度

为了更好的展开对希尔排序叙述，不得不说一下插入排序的时间复杂度。

(1).最坏情况下

最坏情况下：对降序排降序。比如对5 4 3 2 1排升序。
1.假如有n个降序的数。需要排n-1躺。

2.第1趟比较1次，第2趟比较2次，第3躺比较3次。第n-1躺排n-1次。

3.由 等差数列 前n项和公式 (首项 + 末项) * 项数 / 2 得。
T(n) = (n-1)*(1 + n - 1)/2

T(n) = (n-1)*n / 2
所以最坏情况下时间复杂度为(N-1)*N / 2。
4.由大O渐进法表示为O(N²)。

(2).最好情况下

最好情况下：对升序排升序。比如对1 2 3 4 5排升序。
这时，假如有n个元素。只需要对数组遍历一遍就够了，一遍也就是N-1次。
所以时间复杂度为O(N)

(3).基本有序情况下(重点)

例如：2 3 1 5 4

这个时候排升序，大概时间复杂度在 N ~ N² 之间接近 O(N).

5.算法特点

1.是稳定排序
2.代码简单，易实现
3.在数据接近有序 或者 已经有序的情况下，时间复杂度为O(N)

二、希尔排序

因 D.L.Shell 大佬于 1959 年提出而得名。
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。——百度百科

假如给你以下数据和代码，让你写希尔法排 升序，你会怎么写？你会怎么排？

9,8,7,6,5,4,3,2,1

void ShellSort(int* a, int n){	//排序代码}int main(){	int arr[] = { 9,1,2,5,7,4,1,6,3,5 };	int sz = sizeof(arr) / sizeof(arr[0]);	ShellSort(arr, sz);	return 0;}

1.希尔从哪个方面优化的插入排序？

1.因为插入排序有2个特性：当待排序的个数基本有序 和 数据个数较少 时 插入效率较高。
2.所以希尔排序基于这2个特性，先依据间隔(gap)对数据分成各个小组，然后对各组进行预排序，使得数据基本有序，最后再进行一次普通的插入排序使数据整体有序。

2.排序思路

排序实质：实质是采用分组插入的方法。
其实还是插入排序的思路。只是把数据分割为好几组。然后对每组进行插入排序。

整体思路：
1.算法先将要排序的一组数按某个增量gap分成若干组，每组中记录的下标相差gap.
2.对每组中全部元素进行预排序，然后再用一个较小的增量对它进行分组，在每组中再进行预排序。
3.当增量 等于1 时，整个要排序的数被分成一组，排序完成。(这时候相当于 普通的插入排序 了)

3.预排序

以以下10个元素为例。

9,1,2,5,7,4,1,6,3,5

预排序：是对各个间隔(gap) 不为1 的小组 进行直接插入排序。要理解这句话请继续往下看。

关于多少间隔分一组这个问题，怎么分？不要想那么多，按照以下规则分，你就自然懂了。
分组规则：
1.间隔(gap)每次一半一半的分。直到最后gap == 1.
2.这样分其实每次都是折半的，常识来说：折半的时间复杂度都为O(LogN).

#include <stdio.h>//希尔排序void ShellSort(int* a, int n){	//预排序	int gap = n;	while (gap > 1)	{		//每次gap折半		gap = gap / 2;	}}int main(){	int arr[] = { 9,8,7,6,5,4,3,2,1 };	int sz = sizeof(arr) / sizeof(arr[0]);	ShellSort(arr, sz);	return 0;}

以上例子有10个数。那就可以达到5个间隔分一组。2个间隔分一组。还有最后的1个间隔分一组(预排序不包括gap == 1这一组)。

1.gap == 5的分一组进行间隔为5的插入排序。
此时排完序结果为 4 1 2 3 5 9 8 6 5 7

2.gap == 2的分一组，进行间隔(gap)为2的插入排序

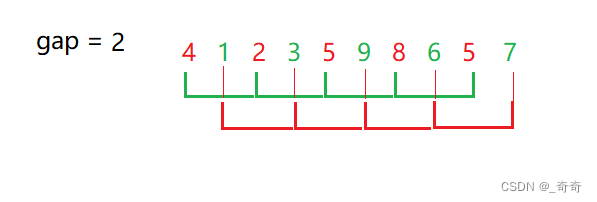
此时排完序结果为 2 1 4 3 5 6 5 7 8 9
这时预排序已经完成。数据基本接近有序开始进行gap为1的插入排序。

4.正式排序

此时gap == 1.直接插入排序

5.整体代码

实质：其实就是加了一个预排序，然后把 插入排序任何为1的地方替换为 gap。

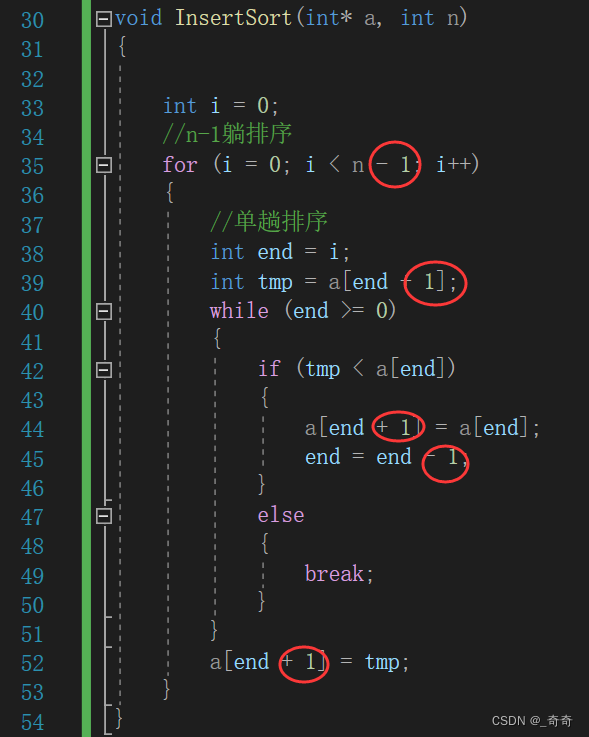
#include <stdio.h>//希尔排序void ShellSort(int* a, int n){	//预排序	int gap = n;	while (gap > 1)	{		gap = gap / 2;		//进行间隔为gap的插入排序		int i = 0;		for (i = 0; i < n - gap; i++)		{			//单趟排序			int end = i;			int tmp = a[end + gap];			while (end >= 0)			{				if (tmp < a[end])				{					a[end + gap] = a[end];					end = end - gap;				}				else				{					break;				}			}			a[end + gap] = tmp;		}	}}int main(){	int arr[] = { 9,8,7,6,5,4,3,2,1 };	int sz = sizeof(arr) / sizeof(arr[0]);	ShellSort(arr, sz);	return 0;}

6.时间复杂度

在严蔚敏老师的书上没有具体说怎么算。因为涉及一些数学上尚未解决的难题。
只给了个结论，时间复杂度为O(N^3/2)

在网上有一个很巧计算方法。只是估算。仅供参考

(1).while循环的复杂度

1.假如有n个数据。n一直初以2.最后要等于1.所以公式为n / 2 / 2 / 2 / 2 / 2… = 1.
2.所以设需要初以 x 个2。也就是要执行 x 次。所以n = 2^x.
所以 x = Log₂n.

3.每次gap减半的 ，也就是while循环的 时间复杂度就是Log₂N

	int gap = n;	while (gap > 1)	{		//每次gap折半		gap = gap / 2;	}

(2).每组gap的时间复杂度

以下说法只是估算。
在预排序阶段。gap很大
1.gap很大很大时，数据跳的很快，差不多时间复杂度为O(N).
正式排序时，gap == 1.
2.gap很小，因为数据接近有序，所以时间复杂度也差不多是O(N)

结论：所以整个代码的时间复杂度为O(N*LogN).

希尔排序空间复杂度也是O(1)，因为还是只需要一个辅助空间tmp。