2022年第十三届蓝桥杯省赛C/C++B组个人题解

2022年第十三届蓝桥杯省赛C/C++B组个人题解

  • 试题 A: 九进制转十进制（数学）
  • 试题 B: 顺子日期（语文）
  • 试题 C: 刷题统计（模拟）
      • 【样例输入】
      • 【样例输出】
  • 试题 D: 修剪灌木（找规律）
    • 【样例输入】
    • 【样例输出】
  • 试题 E: X 进制减法（数学）
    • 【样例输入】
    • 【样例输出】
  • 试题 F: 统计子矩阵（前缀和 + 双指针）
    • 【样例输入】
    • 【样例输出】
  • 试题 G: 积木画（动态规划）
    • 【样例输入】
    • 【样例输出】
  • 试题 H: 扫雷（BFS）
    • 【样例输入】
    • 【样例输出】
  • 试题 I: 李白打酒加强版（三维DP / 回溯）
    • 【样例输入】
    • 【样例输出】
  • 试题 J: 砍竹子
    • 【样例输入】
    • 【样例输出】
  • 总结

试题 A: 九进制转十进制（数学）

A

#include <iostream>#include <cmath> using namespace std;int main() {	cout << 2 * pow(9, 0) + 2 * pow(9, 1) + 0 * pow(9, 2) + 2 * pow(9, 3) << endl;	return 0;}

答案：1478

试题 B: 顺子日期（语文）

B
目前有很多争议，分为 3 种答案：4，5，14
我考试时写的答案是 5
不过我观察到网友更多的答案是 4
而比赛后当天晚上的蓝桥云课说的是 14（非官方）

我来总结一下：

第一种答案：5
看题，在说明 20220123时，说它出现了一个顺子：123。
所以可以认为是只有 123 这一个顺子，而 012 是不算顺子的。
然后在说明 20221023 时又涉及到了 210 这个逆着的顺子，但它说这不是一个顺子日期。因此认为这里更明确了 0 不可以被包括进去，而逆序的可以算是顺子。

2022012320220321202211232022123020221231

第二种答案：4
即认为 012 和逆序的顺子（如 210）都不算是顺子，因此把上面的 20220321 去掉

20220123202211232022123020221231

第三种答案：14
题目说的顺子是：连续的三个数字，并不是三位数。所以 012 也算是顺子。再由第二个例子 20221023 得知：210 这种逆序的不算顺子。
如果要算上 012，那么第二个例子就把 210 这种逆序的给否掉啦

2022012020220121202201222022012320220124202201252022012620220127202201282022012920221012202211232022123020221231

我目前也不知道正确答案，只能等官方解释吧
orz

试题 C: 刷题统计（模拟）

C1

【样例输入】

10 20 99

【样例输出】

8

在这里插入图片描述

陷阱：注意 a, b, n 要用 long long 存
考试时写的代码：只考虑到了 n 要用 long long 存，竟然没用 long long 存 a, b，还没考虑到时间可能还会超限

#include <iostream>using namespace std;int main() {	int cnt = 1;	long long n;	int a, b;	cin >> a >> b >> n;	long long sum = 0;	while (sum < n) {		if (cnt % 7 == 0 || cnt % 7 == 6) {			sum += b;		}		else {			sum += a;		}		cnt++;	}	// 当超出时退出while循环，所以答案需要减一。	cout << cnt - 1 << endl;	return 0;}

赛后优化代码：先取余再暴力

#include <iostream>using namespace std;int main() {	long long a, b, n;	cin >> a >> b >> n;	int week = 5 * a + 2 * b;	long long ans = n / week * 7;	n %= week;	int sum = 0;	for (int i = 1; i <= 7 && sum < n; i++) {		if (i % 7 == 6 || i % 7 == 0) {			sum += b;		}		else {			sum += a;		}		ans++;	}	cout << ans << endl;	return 0;}

试题 D: 修剪灌木（找规律）

D1

【样例输入】

3

【样例输出】

424

D2
首先用暴力找规律，然后再根据规律简化代码

// 暴力代码：来回走两次。注意回的时候要把两个边界去掉。#include <iostream>#include <cstring>using namespace std;const int maxn = 1e4 + 100;int a[maxn];int maxHeight[maxn];int main() {	int n;	while (cin >> n) {		memset(a, 0, sizeof(a));		memset(maxHeight, 0, sizeof(maxHeight));				// 来回走两次		for (int today = 0; today < n; today++) {			for (int i = 0; i < n; i++) {				a[i]++;				if (a[i] > maxHeight[i]) {					maxHeight[i] = a[i];				}				if (i == today) {					a[i] = 0;				}			}		}		for (int today = n - 2; today > 0; today--) {			for (int i = 0; i < n; i++) {				a[i]++;				if (a[i] > maxHeight[i]) {					maxHeight[i] = a[i];				}				if (i == today) {					a[i] = 0;				}			}		}		for (int today = 0; today < n; today++) {			for (int i = 0; i < n; i++) {				a[i]++;				if (a[i] > maxHeight[i]) {					maxHeight[i] = a[i];				}				if (i == today) {					a[i] = 0;				}			}		}		for (int today = n - 2; today > 0; today--) {			for (int i = 0; i < n; i++) {				a[i]++;				if (a[i] > maxHeight[i]) {					maxHeight[i] = a[i];				}				if (i == today) {					a[i] = 0;				}			}		}		for (int i = 0; i < n; i++) {			cout << maxHeight[i] << " ";		}		cout << endl << endl;	}	return 0;}

结果如下：
D2
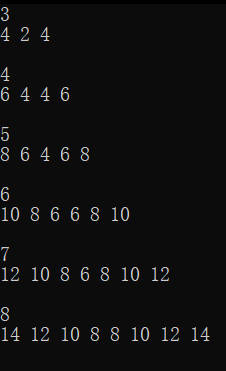
通过找规律可以简化代码：

#include <iostream>using namespace std;int main() {	int n;	cin >> n;	for (int i = 0; i < n; i++) {		cout << max(i, n - i - 1) * 2 << endl; 	}	return 0;}

试题 E: X 进制减法（数学）

E1

【样例输入】

11310 4 031 2 0

【样例输出】

94

E2
比赛时看了一个小时，读不懂题 orz…
这题十分的抽象，很难理解

这里先说明一下问题描述中的 321 是如何转换为 65 的
由题：个位是 2 进制，十位是 10 进制，百位是 8 进制。
题目第一行就说了：进制规定了数字在数位上逢几进一。意思是：个位每数 2 个，十位进 1，十位每数 10 个，百位进 1。
首先定义结果 sum = 0
① 看个位：个位为 1，那么只需数一次即可到 1，然后让结果加上 1，即 sum += 1
② 看十位：十位为 2，因为个位是二进制，所以十位要到 2 的话，就需要经过这样的变换：00 -> 01 -> 10 -> 11 -> 20。可以看出：十位每加 1，个位就需要变换 2 次，所以要使十位变成 2，则一共需要变换 2（十位的值） * 2（个位的进制） 次。然后让结果再加上它，即 sum += 2 * 2
③ 看百位：百位为 3，根据十位的分析，同理得：要使百位变成 3，则需要变换 3（百位的值） * 10（十位的进制） * 2（个位的进制）次。然后让结果再加上它，即 sum += 3 * 10 * 2
综上：321 转换为了 sum = 1 + 2 * 2 + 3 * 10 * 2 = 65

公式：
A = ( a[n - 1] * X[n - 2] * X[n - 3] * … * X[0] ) + ( a[n - 2] * X[n - 3] * X[n - 4] * … * X[0] ) + … + a[0]
B = ( b[n - 1] * X[n - 2] * X[n - 3] * … * X[0] ) + ( b[n - 2] * X[n - 3] * X[n - 4] * … * X[0] ) + … + b[0]
A - B = (( a[n - 1] - b[n - 1] ) * X[n - 2] * X[n - 3] * … * X[0] ) + (( a[n - 2] - b[n - 2] ) * X[n - 3] * X[n - 4] * … * X[0] ) + ( a[0] - b[0] )
优化：（秦九韶算法）
设 d[n - 1] = a[n - 1] - b[n - 1]
A - B = ((( d[n - 1] * X[n - 2] + d[n - 2] ) * X[n - 3] + d[n - 3] ) * X[n - 4] + … d[0] ) …

代码：

#include <iostream>#include <algorithm>using namespace std;const int MOD = 1e9 + 7;const int maxn = 1e5 + 100;int a[maxn];int b[maxn];int main() {	int n, m1, m2, m;	scanf("%d", &n);	scanf("%d", &m1);	// 逆序来存，确保让个位对齐，多余位置的值都是 0 	for (int i = m1 - 1; i >= 0; i--) {		scanf("%d", &a[i]);	}	scanf("%d", &m2);	for (int i = m2 - 1; i >= 0; i--) {		scanf("%d", &b[i]);	}	m = max(m1, m2);	int res = 0;	for (int i = m - 1; i >= 0; i--) {		res = (res * max({ 2, a[i] + 1, b[i] + 1 }) % MOD + a[i] - b[i]) % MOD;	}	printf("%dn", res);	return 0;}

试题 F: 统计子矩阵（前缀和 + 双指针）

F1

【样例输入】

3 4 101 2 3 45 6 7 89 10 11 12

【样例输出】

19

F2
F3
注意 k 已经超了 int 范围（虽然我到不了那就已经超时了，但还是要注意的） 看错了看错了，k 的值是 2.5 * 10 ^ 8，而 int 的范围是 -21 4748 3648 ～ 21 4748 3647 (21 * 10 ^ 8)

方法①：前缀和 + 双指针
首先求出每一列的前缀和，然后利用双指针将若干行切割开

F4
F5

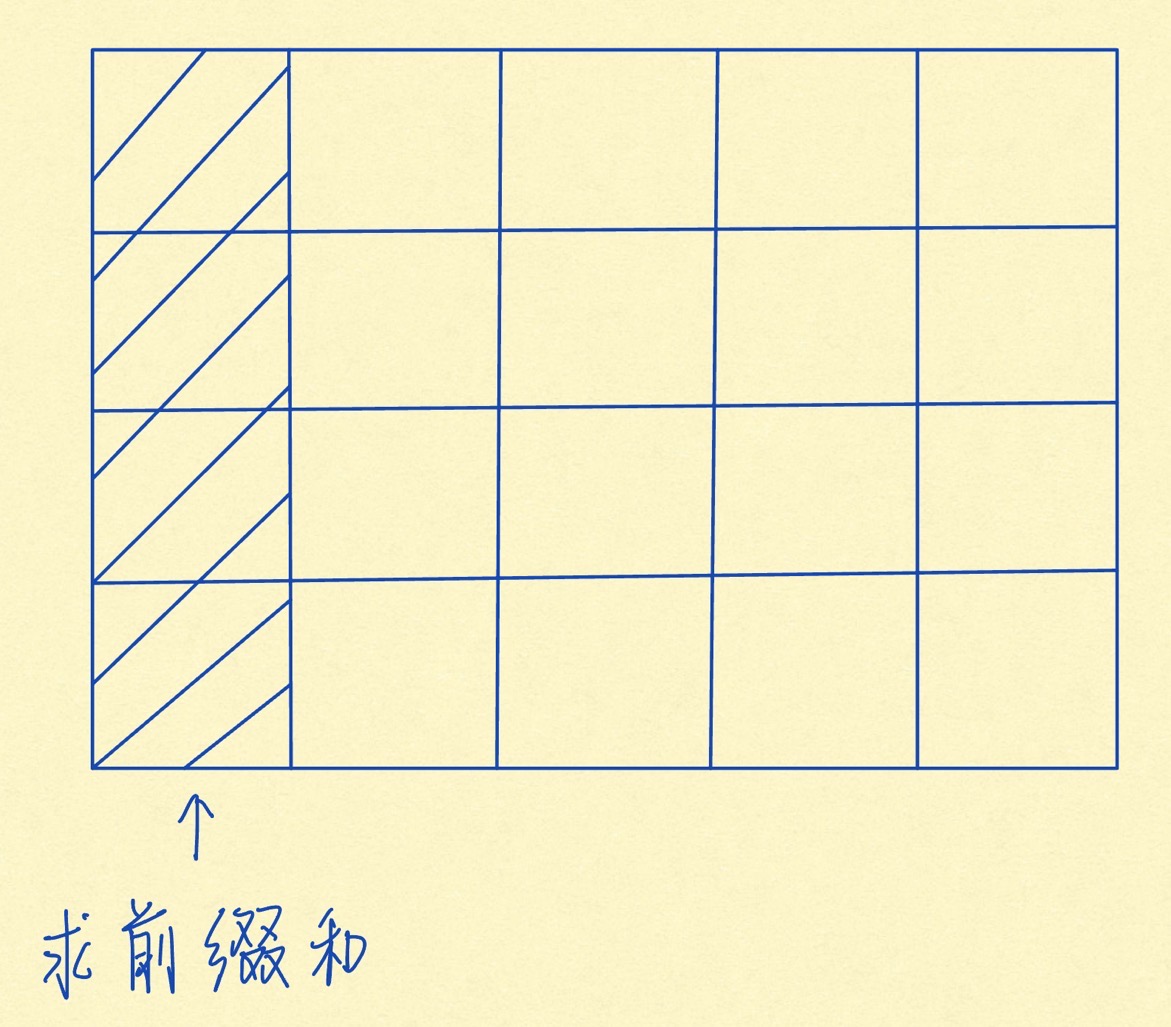
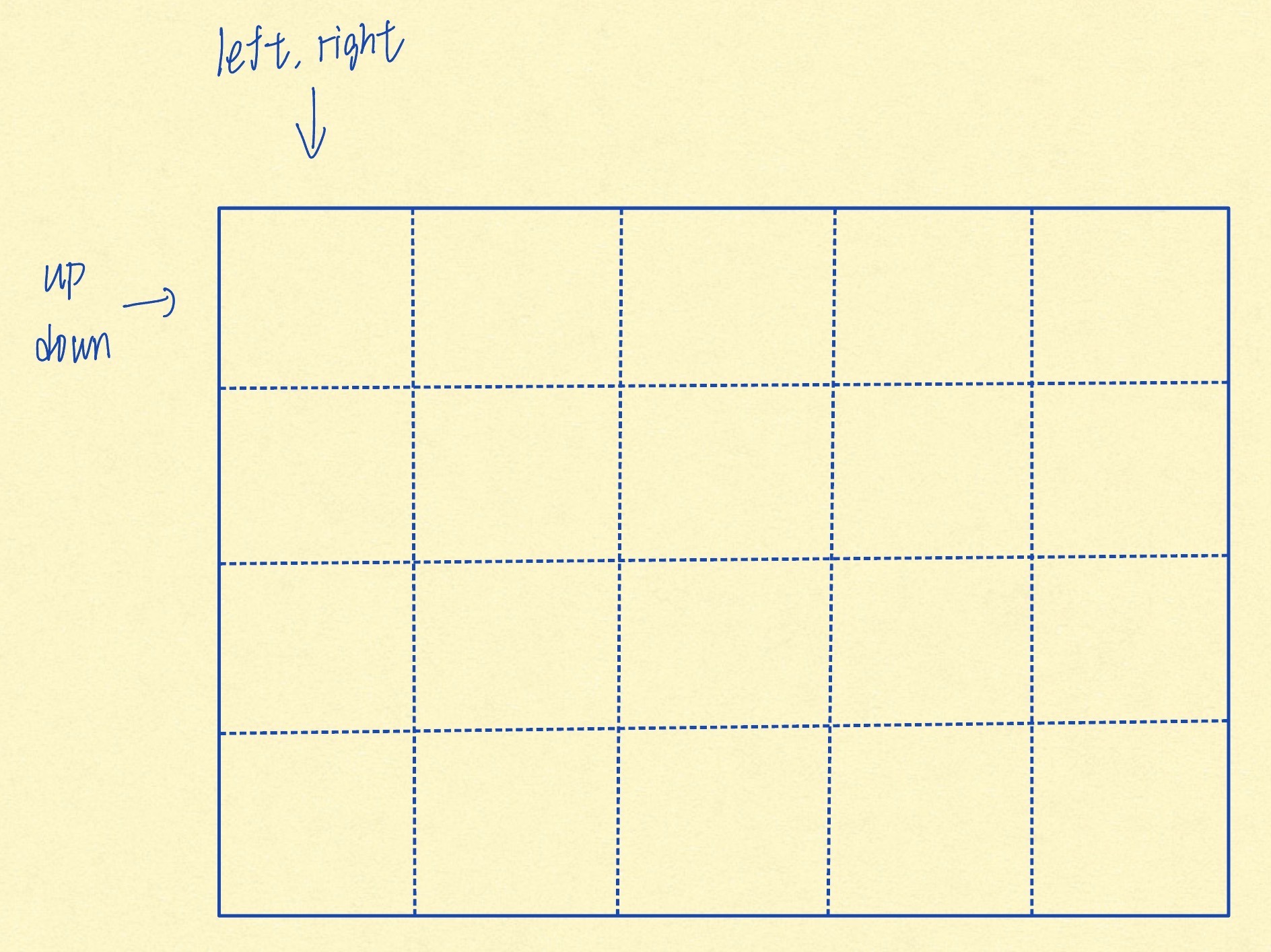
#include <iostream>using namespace std;const int maxn = 505;int s[maxn][maxn];int main() {	memset(s, 0, sizeof(s));	int n, m, k;	scanf("%d %d %d", &n, &m, &k);	for (int i = 1; i <= n; i++) {		for (int j = 1; j <= m; j++) {			scanf("%d", &s[i][j]);			s[i][j] += s[i - 1][j];		}	}	int res = 0;	// 上下边界	for (int up = 1; up <= n; up++) {		for (int down = up; down <= n; down++) {			int sum = 0;			// 左右边界			for (int left = 1, right = 1; right <= m; right++) {				sum += s[down][right] - s[up - 1][right];				while (sum > k) {					sum -= s[down][left] - s[up - 1][left];					left++;				}				res += right - left + 1;			}		}	}	printf("%dn", res);	return 0;}

方法②：暴力（过30%数据，比赛时不会做直接暴力 6 个 for！随便看看就好啦）

#include <iostream>using namespace std;int mat[550][550];int main() {	int n, m;	long long k;	cin >> n >> m >> k;	for (int i = 1; i <= n; i++) {		for (int j = 1; j <= m; j++) {			cin >> mat[i][j];		}	}	long long sum = 0;	long long cnt = 0;	for (int h1 = 1; h1 <= n; h1++) {		for (int h2 = h1; h2 <= n; h2++) {			for (int l1 = 1; l1 <= m; l1++) {				for (int l2 = l1; l2 <= m; l2++) {					sum = 0;					for (int h = h1; h <= h2; h++) {						for (int l = l1; l <= l2; l++) {							sum += mat[h][l];						}					}					if (sum <= k) {						cnt++;					}				}			}		}	}	cout << cnt << endl;	return 0;}

试题 G: 积木画（动态规划）

G1

【样例输入】

3

【样例输出】

5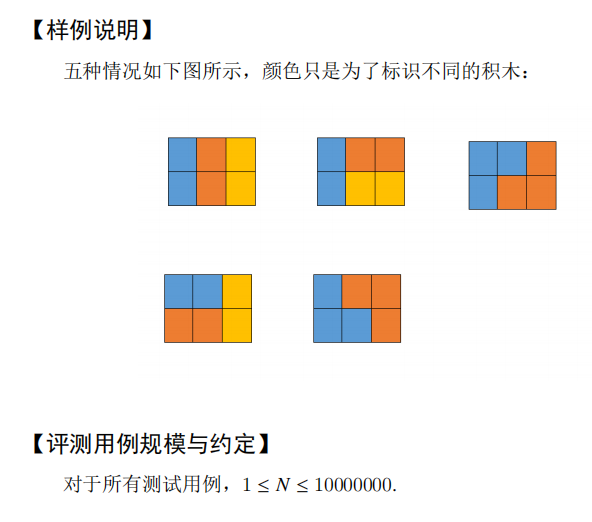

G2
陷阱：注意要取模取模取模，经常有人忘记这回事！！！
（是的，比如说，我倒数第二题就忘记取模了。。。。。
这道题足足用了我三张白纸，我从 n = 1 画到了 n = 6，写了一个小时。
我认为 dp 就是找规律，可是，该死的是我 n = 6 的时候漏画了一种情况（三列横着的摆放），导致一直找不到规律。。。

这道题的规律是，第 n 列可以通过前面的排列，再加上那几种基础的排列得到。
第一种情况：
dp[n] 可以通过 dp[n - 1] 加上普通的一列得到
第二种情况：
dp[n] 可以通过 dp[n - 2] 加上两块横的得到
第三种情况：
dp[n] 可以通过 dp[n - 3] 加上两个三角形的堆起来得到，但要注意的是，这两个三角形的堆叠方式有两种，所以要加上两倍的 dp[n - 3]
第四种情况：（我考试的时候给漏掉了555，不过我现在还是没考虑完整，待完善…
dp[n]可以通过 dp[n - 4] 加上由左右两个各一个三角形，中间若干个横块的组合得到，同第三种情况，这个组合可以倒过来，即有两种堆叠方式，因此要加上两倍的 dp[n - 4]
综上：dp[n] = dp[n - 1] + dp[n - 2] + dp[n - 3] * 2 + dp[n - 4] * 2 （错解，待完善）

#include <iostream>using namespace std;const long long MOD = 1e9 + 7;const int maxn = 1e7 + 100;long long dp[maxn];int main() {	int n;	cin >> n;	dp[0] = 1;	dp[1] = 1;	dp[2] = 2;	dp[3] = 5;	for (int i = 4; i <= n; i++) {		// 注意每次相加后都要取余		dp[i] = (((((dp[i - 1] + dp[i - 2]) % MOD) + dp[i - 3] * 2) % MOD) + dp[i - 4] * 2) % MOD;	}	cout << dp[n] << endl;	return 0;}

试题 H: 扫雷（BFS）

H1

【样例输入】

2 12 2 44 4 20 0 5

【样例输出】

2

H2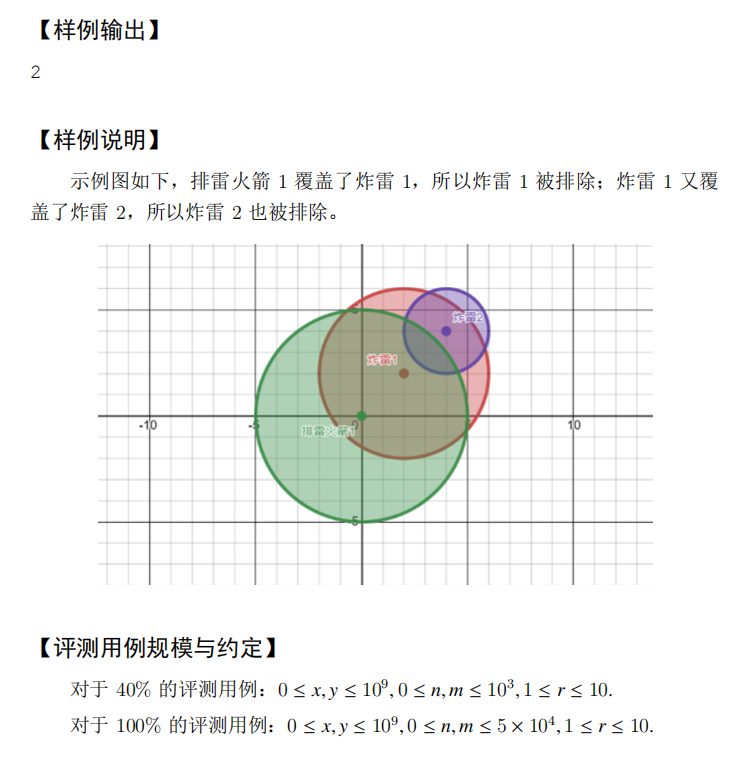
赛前半小时又专门看了眼 BFS，用上了！
陷阱①：一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
陷阱②：有 m 个排雷火箭，但只要求在最后输出一个整数表示答案（我比赛时就输出了 m 次答案…）

#include <iostream>#include <queue>#include <cmath>#include <map>using namespace std;const int maxn = 50100;// 记录坐标和半径int x_pos[maxn];int y_pos[maxn];int radius[maxn];bool vis[maxn]; // 用来记录这个点爆炸了没有// 用于 bfs 的 struct，更方便处理struct point {	int x, y, r;	// 将结构体放入 map 中，需要自己写一个 operator 来排序，因为 map 本身是有序的	bool operator < (const point& p) const {		if (x == p.x) {			if (y == p.y) {				return r < p.y;			}			return y < p.y;		}		return x < p.x;	}};map<point, int> all;double getDis(int x1, int y1, int x2, int y2) {	return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));}int bfs(point begin, int n) {	int cnt = 0;	queue<point> q;	q.push(begin);	while (!q.empty()) {		point cur = q.front();		q.pop();		// 遍历以 2 倍半径为边长的正方形，找到其爆炸所涉及到的炸雷		for (int i = cur.y - cur.r; i <= cur.y + cur.r; i++) {			for (int j = cur.x - cur.r; j <= cur.x + cur.r; j++) {				if (getDis(j, i, cur.x, cur.y) > cur.r) {					continue;				}				point temp;				temp.y = i, temp.x = j;				for (int k = 0; k < n; k++) {					if (!vis[k] && x_pos[k] == temp.x && y_pos[k] == temp.y) {						temp.r = radius[k];						q.push(temp);						cnt++;						all[temp]--;						vis[k] = true; // 标记为已爆炸					}				}			}		}	}	return cnt;}int main() {	int n, m;	cin >> n >> m;	for (int i = 0; i < n; i++) {		cin >> x_pos[i] >> y_pos[i] >> radius[i];		vis[i] = false; // 初始化都还没有爆炸	}	int cnt = 0;	for (int i = 0; i < m; i++) {		point p;		cin >> p.x >> p.y >> p.r;		// 我比赛时输出了 m 次结果，裂开了		// int cnt = 0;		cnt += bfs(p, n);		// cout << cnt << endl;	}	cout << cnt << endl;	return 0;}

试题 I: 李白打酒加强版（三维DP / 回溯）

I1

【样例输入】

5 10

【样例输出】

14

I2
I3
泪目了，写题解发现 我 竟 然 忘记取模了忘记取模了忘记取模了5555555555
大家一定要记得取模！！！

做法一：三维dp（赛后学习的优化方法）

三个维度分别对应：走了多少步、经过了多少家酒馆，酒壶中还剩多少酒
在走到第 n 步时，他可能是从花走来的，也有可能是从酒馆走来的，所以要加上上一步遇到花的所有可能走法，再加上上一步遇到酒馆的所有可能走法。

#include <iostream>using namespace std;const int MOD = 1e9 + 7;const int maxn = 105; long long dp[maxn][maxn][maxn] = { 0 };int main() {	int n, m;	cin >> n >> m;	// 初始化 dp	dp[0][0][2] = 1;	for (int i = 1; i <= n + m; i++) {		for (int j = 0; j <= i; j++) {			for (int k = 0; k <= 100; k++) {				// 遇到了花后抵达第 i 步				dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k + 1]) % MOD;				// 遇到了酒馆后抵达第 i 步				// 当 k % 2 == 0 时才有可能是从酒馆走来的，因为经过酒馆后酒就加倍了				if (j != 0 && k % 2 == 0) {					dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - 1][k / 2]) % MOD;				}			}		}	}	cout << dp[n + m - 1][n][1] << endl;	return 0;}

做法二：回溯法（比赛时用的方法）

年前和年后都练了一段时间的回溯，觉得特别有意思。
赛前半小时还专门看了一眼！！然后考试最后半个小时花了 20min 就写出来了。
本来一下子就写出框架了，不过太着急了，很多题目条件没看清楚，导致找了好久错误，不过还好，这题答案错了的话就是比正确答案大一些，很容易发现错误。

主要错误如下：
① 一共必须要且仅要经过 N 次店，M 次花
② 最后一次遇到的必须是花
③ 最后遇到花后，酒必须喝光
④ 在中途遇到花时，酒不能为空

#include <iostream>#include <string>#include <vector>using namespace std;const int MOD = 1e9 + 7;void backTrack(vector<char>& temp, vector<vector<char> >& ans, int n, int m, int nn, int mm, int jiu) {	if (jiu < 0) return; // 如果遇到花却没酒了，则不符合条件	if (nn > n || mm > m) return; // 如果经过了多于 N 次店、M 次花，则不符合条件	if (temp.size() == n + m) {		if (jiu == 0 && temp.back() == '0') { // 如果最后到达的是店也不符合条件			ans.push_back(temp);		}		return;	}		temp.push_back('0');	backTrack(temp, ans, n, m, nn, mm + 1, jiu - 1);	temp.pop_back();	temp.push_back('1');	backTrack(temp, ans, n, m, nn + 1, mm, jiu * 2);	temp.pop_back();}int main() {	int n, m;	cin >> n >> m;	int jiu = 2;	vector<char> temp;	vector<vector<char> > ans;	backTrack(temp, ans, n, m, 0, 0, jiu);	cout << ans.size() % MOD << endl;	return 0;}

试题 J: 砍竹子

J1

【样例输入】

62 1 4 2 6 7

【样例输出】

5

J2
J3
还剩最后十分钟，没时间做了，看了眼题也确实不会做。

总结

① 注意题目要求，记得取模！
② 注意范围，可能要用 long long
③ 不要在一道题卡太长时间，比如我在 E 题卡了一个小时都没看懂题，就应该早早换题，最后换换思路再回来看或许反而能看懂了

 
版权声明 本文仅代表作者观点，不代表本站立场。
如遇本文系为网络转载到本站发表，图片或文章有版权问题的请联系客服确认后会立即删除文章。
如遇本文系作者授权本站发表，未经许可，不得转载。

--结束END--

有问题投稿请发送至: 邮箱/kf@guangfuqiang.com    QQ/162020580

本文标题: 2022年第十三届蓝桥杯省赛C/C++B组个人题解

本文链接: https://www.guangfuqiang.com/zobk/a16740.html (转载时请保留)

网站首页

返回栏目
今日推荐
新闻举报 返回首页
更多
友情链接
鄂ICP备19019357号-22